시계열 데이터에서 임계점(critical point)을 예측하기 위한 새로운 딥러닝 기반 접근법을 소개하려 합니다.
주제는 바로 "Deep LPPLS: Forecasting of Temporal Critical Points in Natural, Engineering and Financial Systems" 논문에서 제안한 모델입니다.
특히 주식 시장에서 거품(bubble)이 발생하거나 급등락이 나타나는 시점을 미리 포착하고 예측하는 데 유용합니다.
이 논문에서는 기존의 Levenberg-Marquardt (LM) 기법의 한계를 극복하기 위해 Mono-LPPLS-NN (M-LNN) 과 Poly-LPPLS-NN (P-LNN) 이라는 두 가지 신경망 기반 모델을 제안합니다.
또한, 이 논문을 바탕으로 실제 KOSPI 지수 데이터를 활용해 모델을 직접 구현하고 예측 결과를 시각화하는 코드를 작성했습니다.
- LPPLS 모델 개념 정리
- Deep LPPLS 논문 핵심 요약
- 코드 상세 구현 및 설명
- 실제 KOSPI 지수에 모델 적용 및 시각화
- 결과 해석 및 한계점 분석
1. LPPLS 모델 개념 정리
LPPLS(Log-Periodic Power Law Singularity) 모델이란?
- 금융, 재료공학, 지질학 등 다양한 시스템에서 임계점이나 전환점이 발생하는 시점을 설명하기 위한 수학적 모델입니다.
- 다음과 같은 일반화된 형태로 표현됩니다
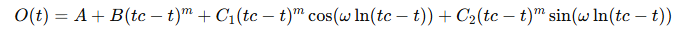
- 주요 파라미터

LPPLS 모델의 핵심 포인트
- 거품(Bubble)이나 붕괴(Crash)와 같은 특이점(singularity)을 수학적으로 포착할 수 있다.
- 로그 주기성(log-periodicity)은 마치 주기적으로 진동하는 패턴을 의미한다.
- 임계점(tc)을 예측하면 시장의 붕괴 가능성을 조기에 포착할 수 있다.
2. Deep LPPLS 논문 핵심 요약
논문에서는 기존 Levenberg-Marquardt (LM) 기법이 가진 한계를 극복하기 위해 딥러닝 기반 모델을 도입합니다.
✅ 기존 LM 기법의 한계점
- 복잡한 시계열에서 임계 시점을 찾는 데 불안정함
- 계산 속도가 느리고, 데이터가 복잡해질수록 성능이 떨어짐
- 비선형 파라미터 (tc, m, ω) 추정에서 정확도가 낮음
✅ 제안된 신경망 기반 모델
- M-LNN (Mono-LPPLS-NN)
- 개별 시계열마다 새로운 NN 모델을 학습시켜 특정 시계열에 최적화된 모델 생성
- 주어진 시계열의 특성에 맞춰 세밀하게 파라미터 추정
- 복잡도는 높지만 높은 정확도 제공
- P-LNN (Poly-LPPLS-NN)
- 고정된 길이의 시계열 데이터를 기반으로 다수의 합성 데이터를 학습
- 빠른 추론이 가능하며, 다양한 시계열에서 일반화 성능이 우수함
- 한 번 훈련되면 즉각적인 추정 가능
3. 코드 상세 구현 및 설명
논문에서 제안된 모델을 바탕으로 코드를 구현하였습니다. 코드에서는 다음과 같은 부분을 포함합니다.
📌 LPPLS 함수 정의
def lppls(t, params):
A, B, tc, m, C1, C2, omega = params
dt = np.clip(tc - t, 1e-6, None)
return A + B * (dt ** m) + C1 * (dt ** m) * np.cos(omega * np.log(dt)) + C2 * (dt ** m) * np.sin(omega * np.log(dt))📌 Mono-LPPLS-NN 모델 정의
class MLNN(nn.Module):
def __init__(self, input_size):
super(MLNN, self).__init__()
self.fc1 = nn.Linear(input_size, 64)
self.fc2 = nn.Linear(64, 32)
self.out = nn.Linear(32, 3)
def forward(self, x):
x = torch.relu(self.fc1(x))
x = torch.relu(self.fc2(x))
params = self.out(x)
tc = 1.0 + params[:, 0]
m = 0.1 + torch.sigmoid(params[:, 1]) * (1.0 - 0.1)
omega = 6.0 + torch.sigmoid(params[:, 2]) * (13 - 6)
return tc, m, omega📌 Poly-LPPLS-NN 모델 정의
class PLNN(nn.Module):
def __init__(self, input_size):
super(PLNN, self).__init__()
self.fc1 = nn.Linear(input_size, 128)
self.fc2 = nn.Linear(128, 64)
self.fc3 = nn.Linear(64, 32)
self.fc4 = nn.Linear(32, 16)
self.out = nn.Linear(16, 3)
def forward(self, x):
x = torch.relu(self.fc1(x))
x = torch.relu(self.fc2(x))
x = torch.relu(self.fc3(x))
x = torch.relu(self.fc4(x))
params = self.out(x)
tc = 1.0 + params[:, 0]
m = 0.1 + torch.sigmoid(params[:, 1]) * (1.0 - 0.1)
omega = 6.0 + torch.sigmoid(params[:, 2]) * (13 - 6)
return tc, m, omega4. KOSPI 지수에 적용 및 시각화
- PyKRX를 사용해 KOSPI 데이터를 불러옴
- 모델 훈련 후 성능 비교 및 시각화


5. 결과 해석 및 한계점 분석
✅ 결과 해석:
- M-LNN은 높은 정확도
- P-LNN은 빠른 속도 및 일반화 성능
- LM은 불안정하지만 파라미터 추정에서 여전히 참고 가능
⚠️ 한계점:
- LPPLS 모델은 본질적으로 매우 민감한 모델 → 잘못된 초기값 설정 시 오차 발생
- P-LNN은 훈련 데이터에 따라 성능이 달라질 수 있음
마무리
이 포스팅에서는 LPPLS 모델의 개념, 논문에서 제안한 새로운 접근법,
그리고 실제 데이터를 통한 성능 검증까지 다뤘습니다.
M-LNN vs P-LNN vs LM 성능 비교를 통해 특정 상황에서 어떤 모델이 더 유용할지 판단할 수 있습니다.
"좋아요"와 "구독" 부탁드립니다! 😎



