AI/DeepLearning
DNN 회귀 모델 스크레치 구현 및 역전파 완전 정리로 빠르게 복습하기
Quantrol
2025. 3. 24. 14:27
반응형
1. 개요
본 글에서는 Python으로 딥러닝 기반 회귀 모델을 스크래치로 구현하고, 역전파 과정에서 발생하는 수식을 체계적으로 정리한다. 특히, 체인룰(Chain Rule)에 따라 손실 함수, 출력층 및 은닉층에서의 기울기 계산이 어떤 논리로 이루어지는지 명확히 설명한다. 가중치와 편향의 미분이 어떻게 전개되는지, 행렬 미분에서 전치 연산이 필요한 이유를 포함해 완벽하게 이해하는 것을 목표로 한다.
2. 회귀 모델 구조 및 데이터 생성
기본적인 회귀 문제는 다음과 같은 3차 다항식을 따르는 데이터셋을 생성하는 것으로 시작한다.
import numpy as np
import matplotlib.pyplot as plt
# 데이터 생성
np.random.seed(42)
X = np.random.rand(100, 1) * 10 - 5 # -5 ~ 5 사이의 값
y = 0.5 * X**3 + 3.0 * X**2 - 1 * X + 3 + np.random.randn(100, 1) * 5
# 시각화
plt.scatter(X, y, alpha=0.6)
plt.title("Generated Data")
plt.show()- X → 입력 데이터
- y → 출력값 (3차 다항식 + 노이즈)
3. 모델 구조 정의
모델 구조는 입력층, 은닉층 2개, 출력층으로 구성된다. 활성화 함수는 ReLU를 사용하며, 손실 함수는 평균 제곱 오차(MSE)로 설정한다.
모델 구조
- 입력층 → 은닉층1 → ReLU → 은닉층2 → ReLU → 출력층
- 가중치 초기화는 He 초기화 사용
He 초기화
가중치는 다음과 같이 He 초기화를 통해 초기화한다.

class NeuralNetwork:
def __init__(self, input_dim, hidden_dim, output_dim):
self.W1 = np.random.randn(input_dim, hidden_dim) * np.sqrt(2. / input_dim)
self.b1 = np.zeros((1, hidden_dim))
self.W2 = np.random.randn(hidden_dim, hidden_dim) * np.sqrt(2. / hidden_dim)
self.b2 = np.zeros((1, hidden_dim))
self.W3 = np.random.randn(hidden_dim, output_dim) * np.sqrt(2. / hidden_dim)
self.b3 = np.zeros((1, output_dim))4. 순전파 (Forward Propagation)
순전파 과정은 다음과 같다.

코드 구현
def forward(self, X):
self.Z1 = X @ self.W1 + self.b1
self.A1 = np.maximum(0, self.Z1) # ReLU
self.Z2 = self.A1 @ self.W2 + self.b2
self.A2 = np.maximum(0, self.Z2) # ReLU
self.Z3 = self.A2 @ self.W3 + self.b3
return self.Z35. 손실 함수 정의
손실 함수로 평균 제곱 오차(MSE)를 사용한다.
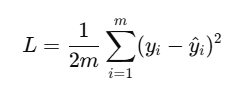
미분이 깔끔해지도록 상수 1/2 를 포함시킨다.
코드 구현
def compute_loss(self, y_pred, y_true):
m = y_true.shape[0]
loss = (1 / (2 * m)) * np.sum((y_pred - y_true) ** 2)
return loss6. 역전파 (Backpropagation)
역전파는 체인룰을 통해 출력층 → 은닉층2 → 은닉층1 방향으로 기울기를 전달하며 진행된다.
6.1 출력층의 역전파

코드 구현
dZ3 = y_pred - y_true
dW3 = (1 / m) * self.A2.T @ dZ3
db3 = (1 / m) * np.sum(dZ3, axis=0, keepdims=True)6.2 은닉층의 역전파

코드 구현
dA2 = dZ3 @ self.W3.T
dZ2 = dA2 * (self.Z2 > 0)
dW2 = (1 / m) * self.A1.T @ dZ2
db2 = (1 / m) * np.sum(dZ2, axis=0, keepdims=True)은닉층1의 경우도 동일한 구조로 적용된다.
코드 구현
dA1 = dZ2 @ self.W2.T
dZ1 = dA1 * (self.Z1 > 0)
dW1 = (1 / m) * X.T @ dZ1
db1 = (1 / m) * np.sum(dZ1, axis=0, keepdims=True)6.3 가중치 업데이트
경사 하강법을 적용한다.
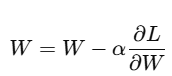
코드 구현
self.W3 -= learning_rate * dW3
self.b3 -= learning_rate * db3
self.W2 -= learning_rate * dW2
self.b2 -= learning_rate * db2
self.W1 -= learning_rate * dW1
self.b1 -= learning_rate * db17. 학습
학습 과정에서 순전파 → 손실 계산 → 역전파 → 가중치 업데이트가 반복된다.
8. 결론
출력층에서의 전치 연산은 행렬 미분의 일반적인 규칙에서 기인하며, 편향에 대한 합 연산은 모든 샘플에 대한 편향이 동일하게 적용되기 때문이다. 이 구조를 이해하면 딥러닝 모델의 구조와 학습 과정이 명확히 보인다.
반응형